3Blue1Brown《直观解释Transformer》

3B1B讲深度学习和Transformer的视频也很出名了,国内许多讲相关概念(注意力、词嵌入等等)的文章都会或多或少的引入一些这个系列视频的截图和观点
机器学习
机器学习:采用数据驱动,反馈到模型参数,指导模型行为
- 深度学习是机器学习中的一种,旨在运用反向传播算法解决大规模数据集下的过拟合和欠拟合问题
- 机器学习的理念是不要在代码中明确定义如何执行一个任务
机器学习最简单的用法就是线性回归,找到数据拟合曲线
GPT
Generative Pre-trained Transformer(生成式的、预训练的Transformer模型)
Transformer是一种序列转导模型,给定一段初始文本,然后根据概率预测下一个词,并在选择之后,将追加上新词的文本重新作为输入继续预测下一个词
Transformer模型步骤
这个参考我另外两篇讲《The Anotated Transformer》和《Attention Is All You Need》的报告更好,其中的
词嵌入
Embedding Layer
嵌入层矩阵中的每一列代表了每个token对应的向量,和其他层一样需要在训练过程中根据数据学习

在模型训练过程中调整权重时,最终得到的嵌入向量在空间中的方向代表着某种语义含义
- 举例来说,如果在向量空间中找到代表男人和女人的向量,这两个向量的向量差,和国王和女王的向量差非常接近
- 于是当我们要找到代表了女性国王的词汇时,可以得到
,然后寻找离这个位置最近的那个向量 - 另一个例子是
点积可以用于衡量两个向量的对齐程度
- 点积为正时,说明两个向量方向相近
- 点积为零时,说明两个向量垂直
- 点击为负时,说明两个向量方向相反
- 举例来说,,复数名词与复数的点积往往要比单数名词与复数的点积大
GPT-3的词汇库中包含50257个token的向量,每个向量都是12288维的,因此单嵌入层就包含了6.17亿个权重
由于嵌入层的token向量是直接对应到具体token上的,因此并不包含上下文信息,在后续网络的处理过程中,会使这些向量获得更丰富的含义
- 由于网络一次只能处理特定数量的向量,因此Transformer在预测下一个词时能结合的文本量也是有限的,这个叫做上下文长度(GPT-3的上下文长度为2048)
Unembedding Layer
在经过一系列处理后,我们会在最后一层的矩阵得到一系列向量,要得到下一个单词,首先要将解嵌层矩阵和最后一列向量相乘,以GPT-3为例,得到一个50k维的新向量,该向量代表了词汇库中下一个单词出现的概率权重,并经过softmax函数归一化为概率值后得到每个token出现的概率
- 如果将最后一层矩阵的第N列向量而非最后一列与解嵌层矩阵相乘,那么得到的结果就代表了第N个位置的token对下一个位置的token的预测
- 显然地,解嵌层的矩阵行数对应模型中的词汇库中的token数量(50257),列数对应每个token向量的维度(12288),这一点和嵌入层矩阵恰好是相反的

softmax函数
要将一组数字作为概率分布看待,那么应当满足以下两个条件
- 每个数字都介于0到1之间
- 所有数字之和恰好为1
softmax对于第n项x的操作如下
保证每个数字满足以上概率分布规则
此外,可以引入一个额外的参数T(温度)
当T越大时,会给予较小的值更多的权重,使得分布更加均匀
显然地,当T=0时,模型总是会选择最可能的那个词,而当T越高时,模型更愿意选择可能性较低的词,赋予模型更多的“创造力”,但反过来也更容易导致模型输出文本的逻辑混乱
- 一般来说,T不会大于2,这是一个人为的限制,防止模型生成过于荒诞的内容
在softmax函数中,输入向量被叫做Logits,而输出向量则被叫做Probabilities(即概率)
- logits一般被用来指那些原始的、未经过归一化的输出
自注意力机制
在嵌入层将token转换为向量后,向量中的信息并不包含上下文信息,举例来说:
- American shrew mole
- One mole of carbon dioxide
- Take a biopsy of the mole
三句话中的mole在经过嵌入层后得到的向量是完全相同的,因为嵌入层本质上是没有上下文信息的查找表——在注意力机制,周围的信息才会传递给该向量
总的来说,注意力机制允许嵌入向量彼此传递所蕴含的信息,并精细化每个token的含义
这里的传递范围可以达到很远,举例来说,当我们输入了一整本的推理小说,并在最后一句话给出therefore,the murder was时,最后一个词(也就是was)向量所蕴含的信息包含了整本小说的上下文,远远超出了这个词本身所拥有的含义
单头注意力机制
注意力机制的核心在于对于一个token A,在它之前的token中找到与该token A相关性最大的token B,并基于B的信息和位置修正A的信息
我们给定两个矩阵
- 这两个矩阵的列数都是12288,即嵌入向量的维度,因为后面要和嵌入向量做乘法运算
- 这两个矩阵的行数都是128行,对应键——查询空间维度
令词向量
令词向量
根据上文提到的,我们计算查询向量和键向量的点积,该数值的大小即可代表两个词向量之间的相关性
- 当token A(可能是一个名词)的Query和token (可能是A前的一个形容词)B的Key的点积很大时,我们可以说A注意到了B
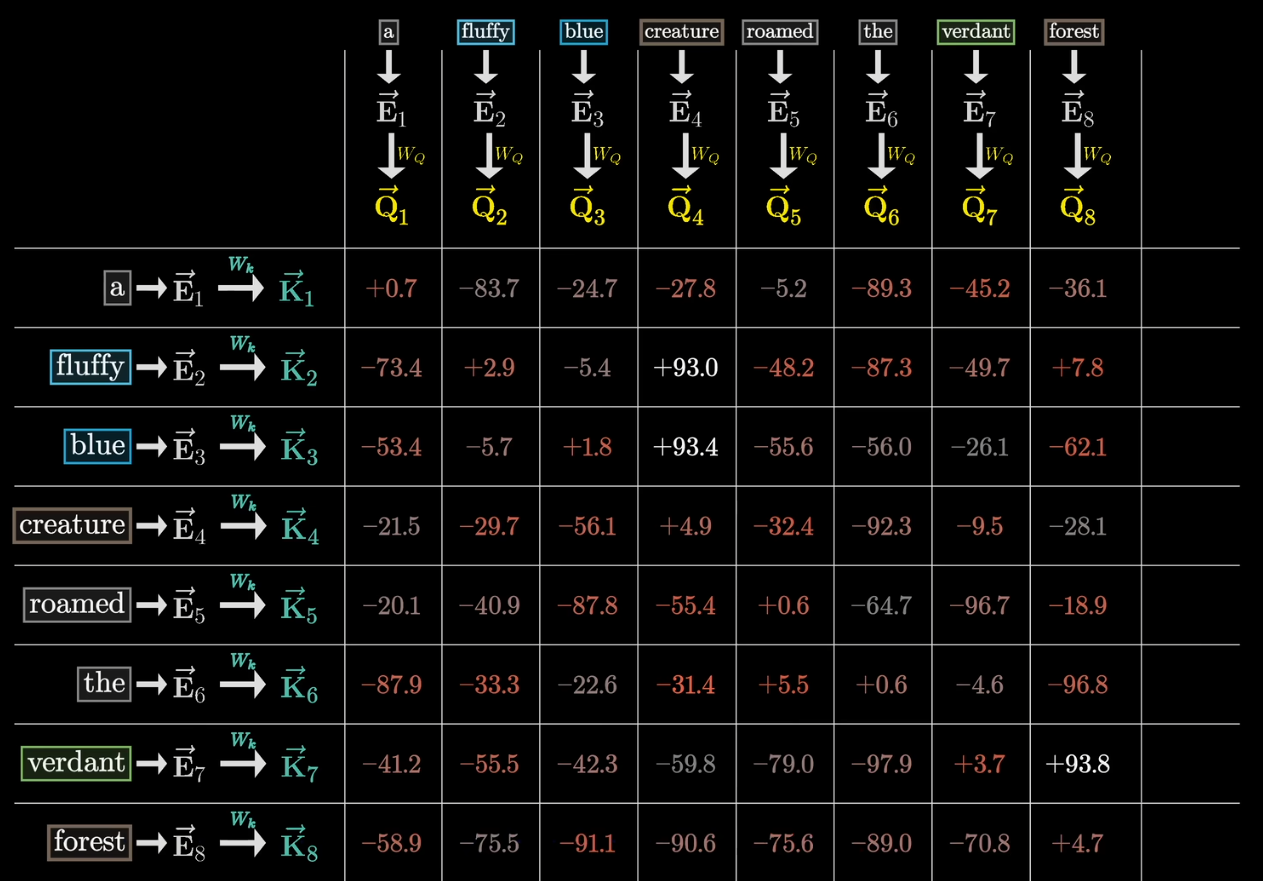
这个点积表我们叫做注意力模式(Attention Pattern)
给定一个新的矩阵
- 同样地,列数是12288,即嵌入向量的维度,后面要和嵌入向量做乘法运算
- 行数也是12288,因为最终输出的结果是嵌入向量的变化量,因此维度应当相同
- 因此值矩阵的参数量要比键矩阵和查询矩阵多出几个数量级
令词向量
接下来,对于词向量
$$
E_N=E_N+\sum^{M=1}{N}Attention(Q_N,K_M,V_M)\
E_N=E_N+\sum^{M=1}{N}(V_M\times Weight)
$$
显然地,我们可以用
- 原论文中考虑到了数据的稳定性,在softmax之前还将点积结果除以了
接下来,还有一点要考虑的,当我们计算相关性时,实际上是可以并行计算的,举例来说
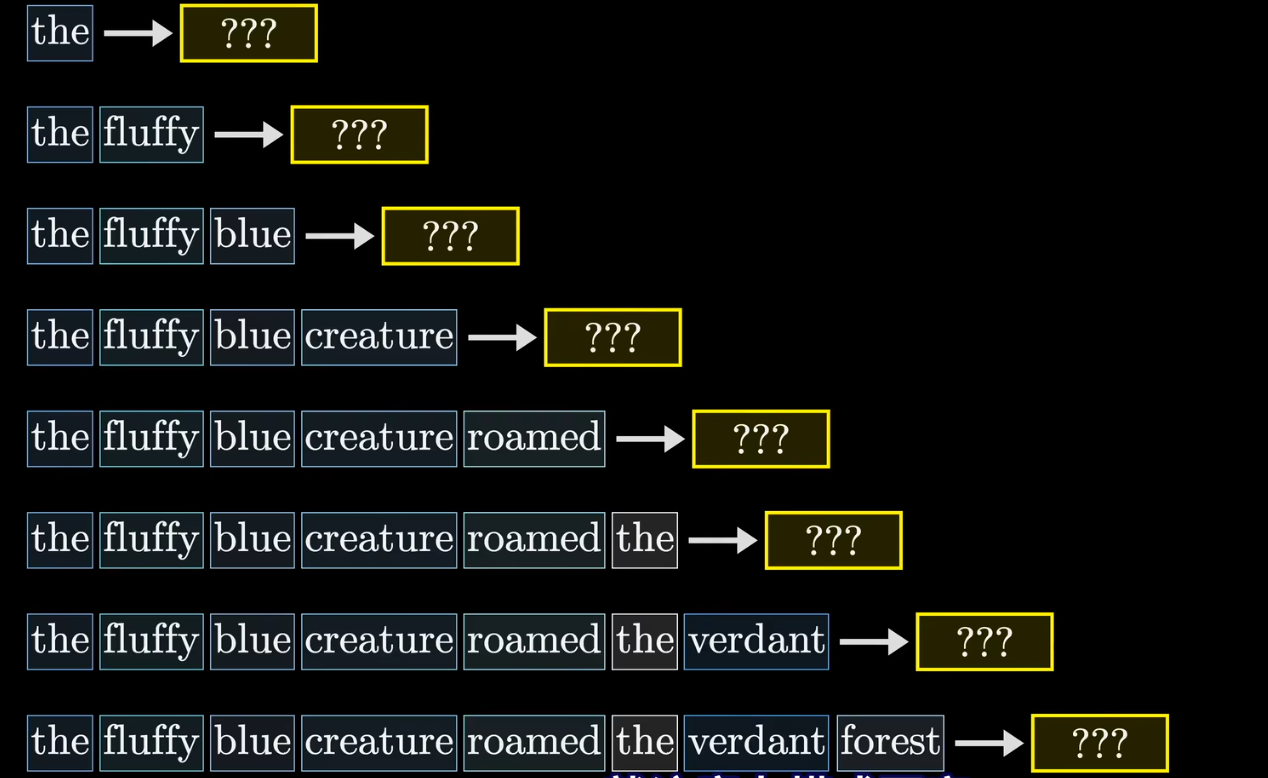
对于the fluffy blue creature roamed the verdant forest这个已经得到的输出,我们可以并行地对它的所有子序列再去预测一次来提升训练效率,但是在这种情况下,当我们考虑去预测the fluffy blue creature这个子序列时,roamed the verdant forest这个子序列就不应当在注意力计算的过程中占有任何的权重(因为预测the fluffy blue creature时,我们假设后面的内容还没有被生成)
因此,在计算注意力的过程中,我们应当保证在查询当前位置的token时,不去考虑在当前位置之后的token的相关性,或者说不能让后面的token影响前面的token,即对于
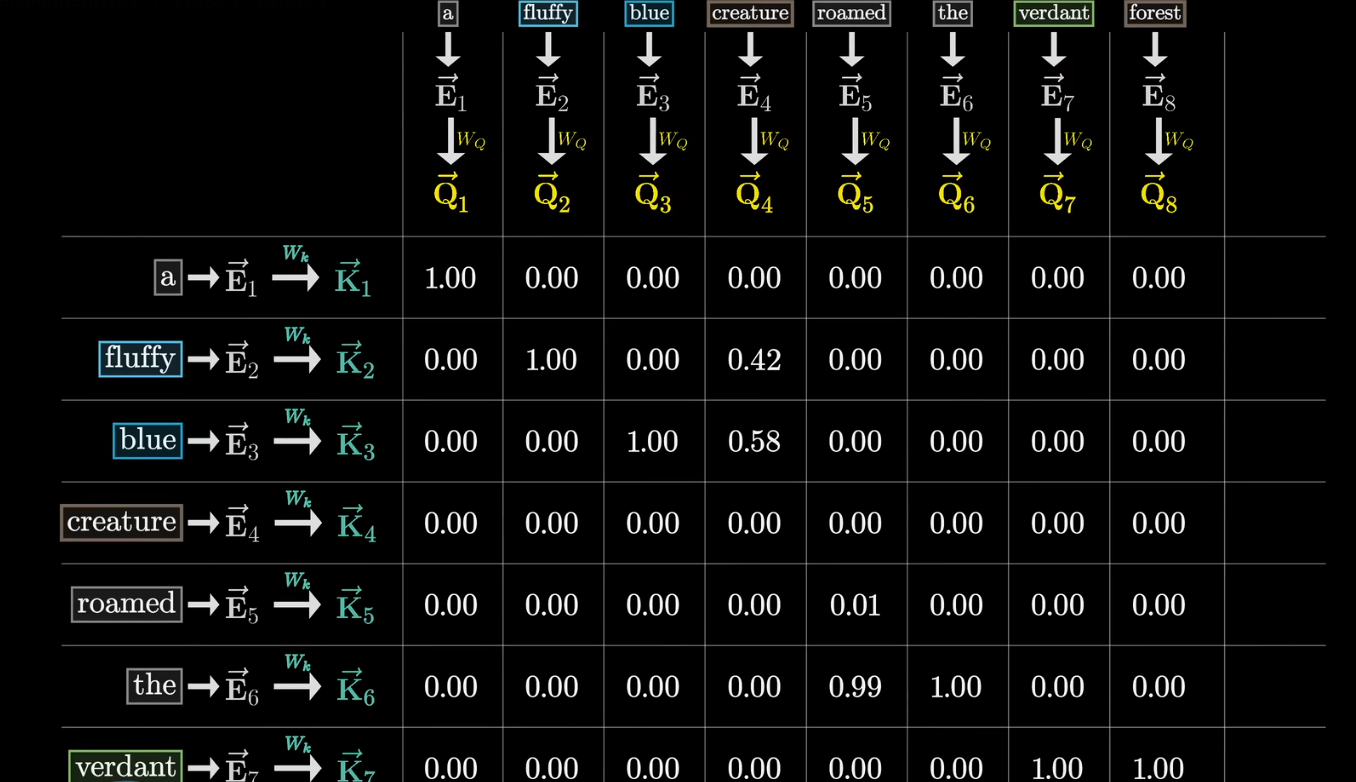
要注意的是,这一步一定要在softmax之前做,否则的话对于一个Query列而言,所有Key向量权重之和就不为1了
一个可行的操作是,先将注意力模式表中下三角位置的值都设置为负无穷,这样在softmax后这些值就都接近于0,这一步被叫做掩码
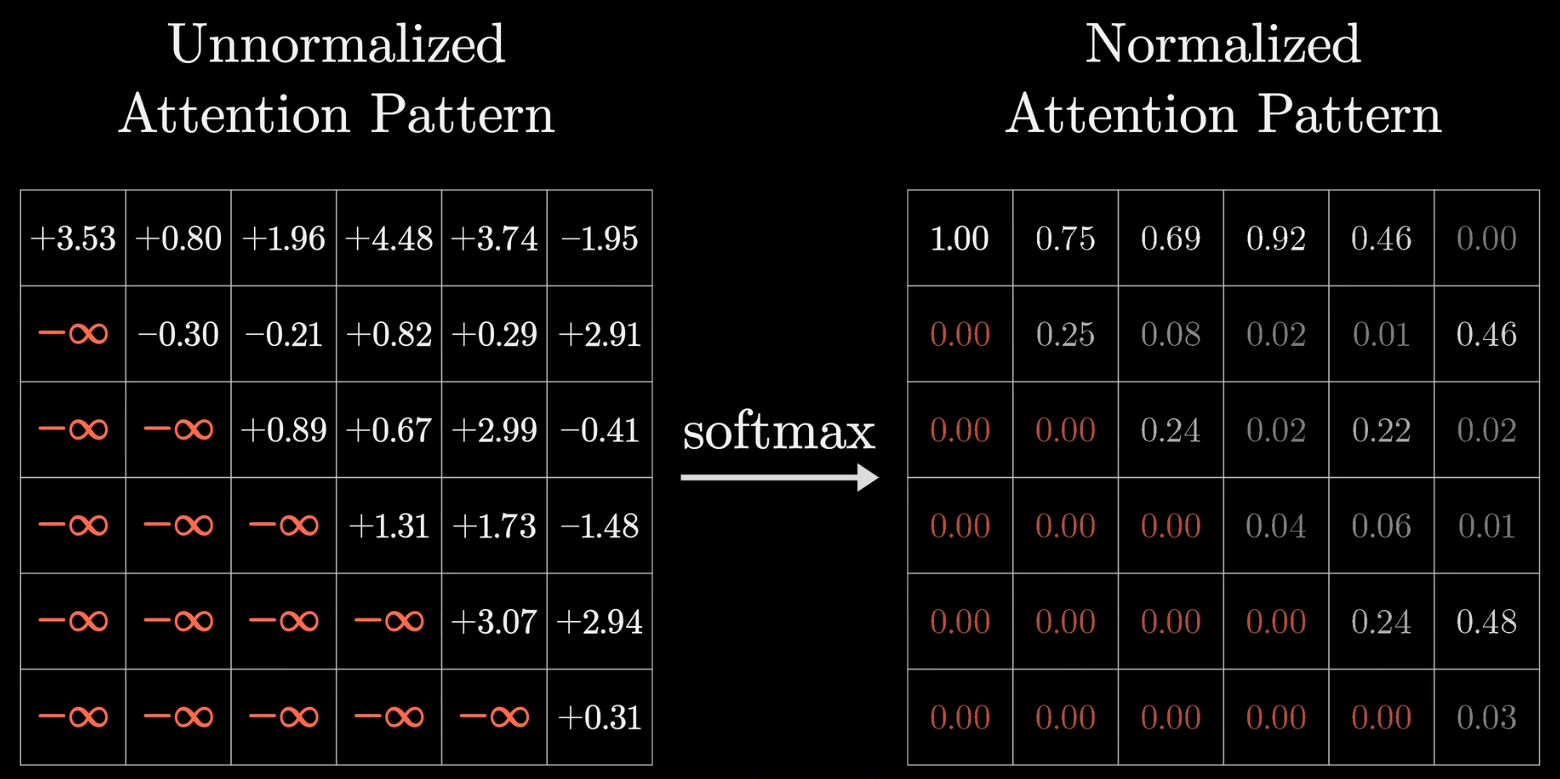
也是因为并行训练的原因,掩码在训练过程中比在运行过程中更加重要,但是两个过程中都会用到掩码,来防止后面的token对前面的token产生影响
不难发现,注意力模式表的大小等于上下文长度的平方,因此大语言模型的瓶颈往往都在上下文长度上
在得到注意力模式表后,我们已经可以算出每个token B对于token A的影响的权重:
将该权重乘以token B的值向量,就是token B应当对token A产生的影响
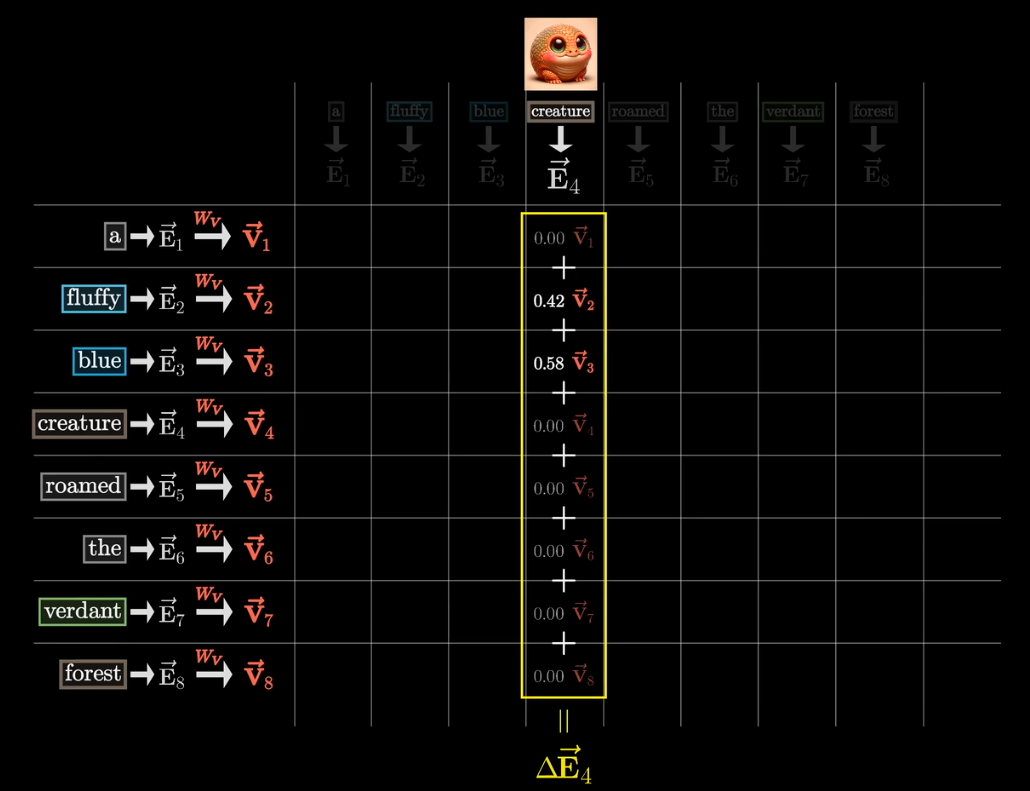
实际过程中,对每一列分别计算值向量的加权和,第N列就代表第N个向量的变化量,将其分别加到对应的嵌入向量上,从而得到一个更准确的新的嵌入向量
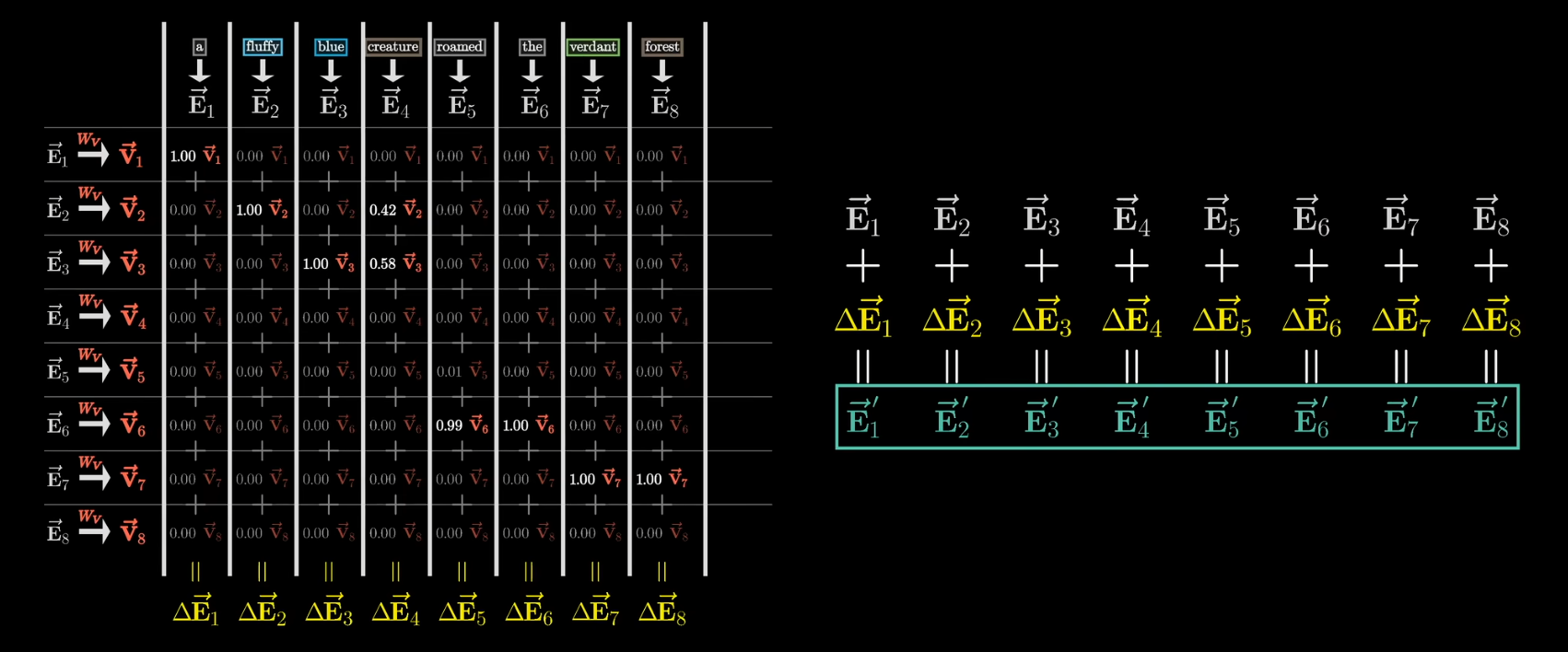
值矩阵压缩
不难注意到,单个传统的值矩阵的参数量就有
一个更好的办法是将值矩阵拆分为两个较小的矩阵相乘,并将这两个矩阵仍然看作一个线性变换整体

其中右侧的矩阵一般行数等于键——查询空间的维数,即128,负责将嵌入向量降维到较小的空间
左侧矩阵则负责将结果从小空间重新映射回嵌入空间,得到实际用于更新的向量
这个操作在线性代数中被叫做大矩阵的低秩分解
在这种情况下,值矩阵的参数量被压缩到了

单个注意力头具有约630w个参数
交叉注意力
要注意的是,这里的注意力机制集中讨论自注意力机制,即数据集对自身进行注意
另一种是交叉注意力机制,与自注意力的不同点在于键和查询作用于不同的数据集
- 如不同语言的翻译,文本语音转录等
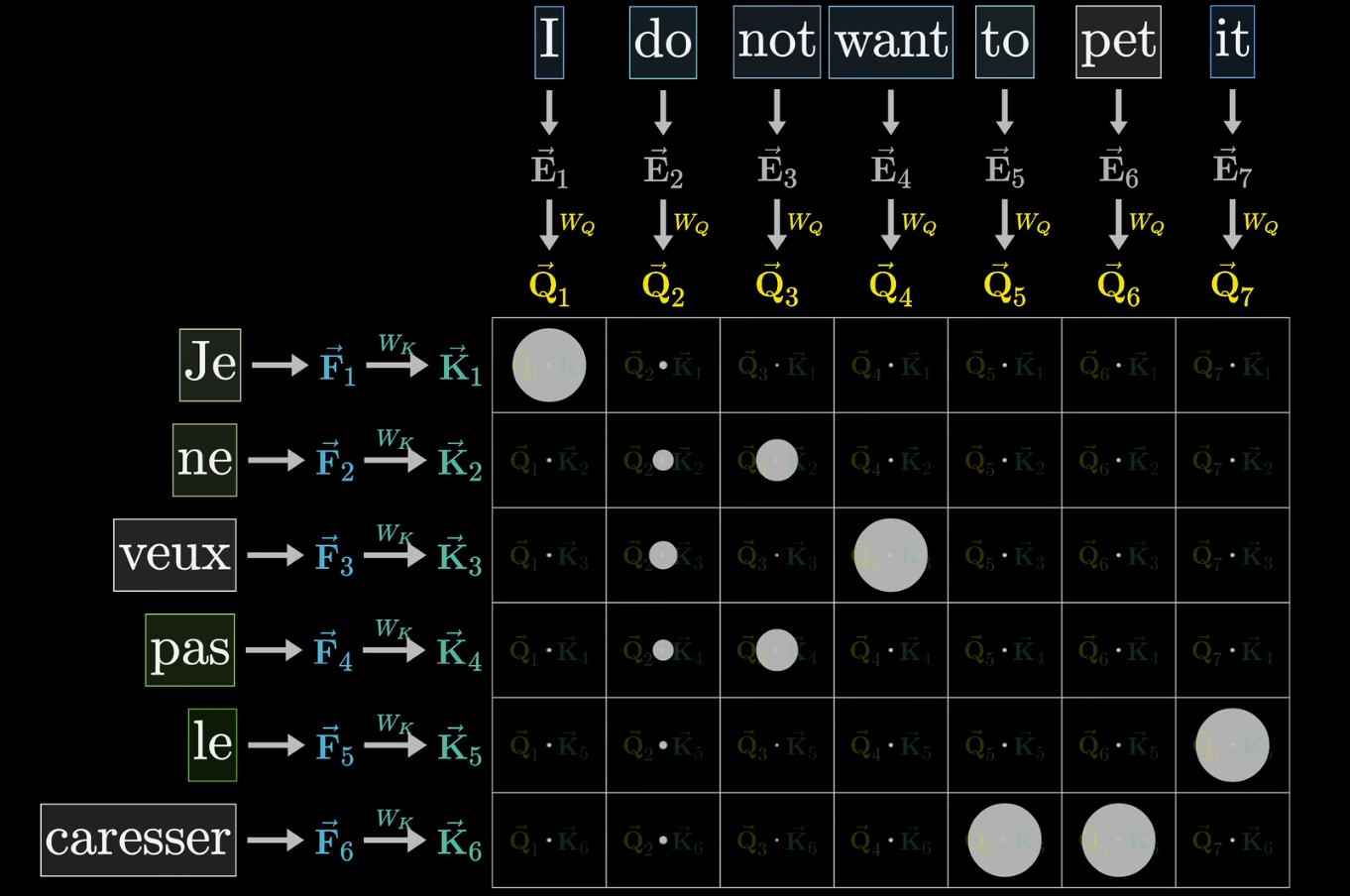
在这种情况下因为不存在后文影响前文的问题,所以往往不需要进行掩码
多头注意力
注意力往往不止局限于语法层面上
- 例如他们撞毁了出现在车前面,则意味着车的形状发生了改变
对于每一种不同的上下文更新方式,键和查询矩阵的参数都要有所改变,来捕捉不同的注意力模式,而值矩阵也要根据影响方式的不同有所调整
Transformer的一个完整的注意力层中包含多个注意力模块,大量并行地进行注意力计算,每个头都有不同的键、查询和值矩阵
- 注意力机制本身的成功并不在于他的行为,而是他第一次有了可并行性,允许GPU在短时间进行大量并行运算,极大地提高了模型规模
- 深度学习的一个重要经验就是:只靠扩大模型规模,就能为模型性能带来质的飞跃
GPT-3中每个注意力层包含93个注意力头,也就是96组不同的键/查询矩阵,来产生96种不同的注意力模式,每个头也有独特的值矩阵
- 也就是说,对于每一个token,每个值矩阵都会给出一个变化量,而对于该token的输出,则是将嵌入向量和每个变化量分别相加,得到该token的输出向量

在这种情况下,每个注意力层最终的参数量是单头注意力的参数乘以96,即大约6亿个参数
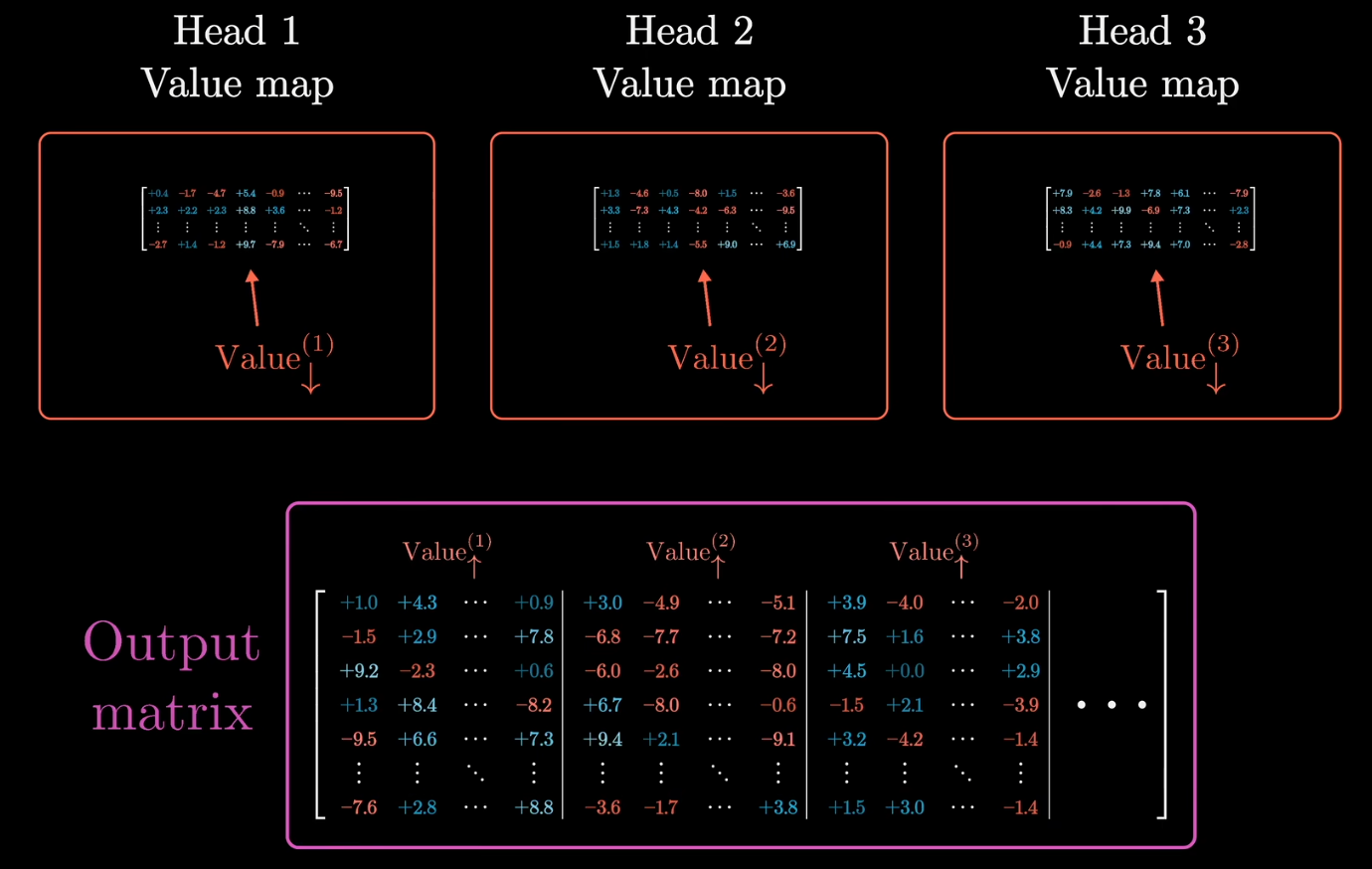
回到上文提到的值矩阵压缩

我们将值矩阵拆分为了一个降维矩阵(右侧)和升维矩阵(左侧)
但是实际上论文在多头注意力的实现中,将每个单头注意力模块的升维矩阵拼接在了一起,形成一个输出矩阵(这里指的是多头注意力层的输出),而单个注意力头的值矩阵指的实际上只有右侧的降维矩阵部分